2023/08/1
顧客情報管理
相関分析とは?回帰分析との違いや具体的な手法をわかりやすく解説

皆さん、何か物事の結論を分析、解析する際にどの変数がどの程度影響を及ぼしているのかについてどのように検討されていますか。
本記事では相関分析とは?という部分において、相関関係のご説明から回帰分析との違いまでを含めてご紹介させて頂きます。
目次
相関分析とは何か
ここでは相関分析とは何か、相関分析の定義や、分析結果として確認する事ができる相関関係、相関係数等の基本的な用語についてご説明します。
相関分析の定義
そもそも相関とは「分析対象とする一方が変化すればそれに伴って別事象も同様に変化する」であったり、「別事象は何も変化がなかった」といったような、事象同士が互いに関係を持つことを指します。
相関分析とは相関関係を把握するために用いる分析となり、2つの要素における関係性を読み解く際に用いられる分析手法です。そのため、相関分析を行うことで分析対象とされる2要素は関係があるのか、また互いにどのように影響し合っているのか等を確認する際に利用します。
相関関係と相関係数とは
相関関係とは、「一方の変数が変化すると、もう一方が増加または減少する2要素間の関係」を指します。例えば、視力が0.3以下の人を対象にアンケートをとると、一日に閲覧するPCやスマートフォンの時間数に比例して多い傾向が見えた場合、相関関係があると言えます。なお、相関係数とは「2種類のデータ間において、どの程度関係性が強いかを表す指標であり、-1から+1の間の数値で表します。
また、相関関係は因果関係とよく比較されますが、違いとしては根本的な原因か否かについて問わず、数値敵に関係が見えるか否かという部分でのみ関係性を計るという部分です。
因果関係は逆に、「原因とそれによって生じる結果との関係」を表します。
相関分析の3つの相関
では、相関分析を行った結果表現される「正の相関」「負の相関」「無相関」の3つの相関について確認しましょう。
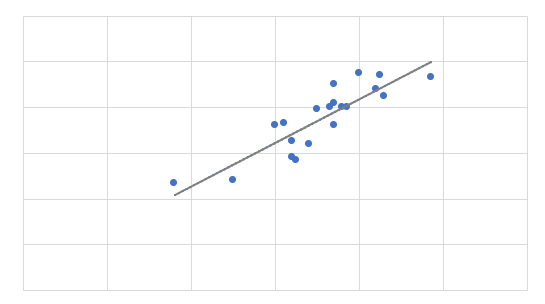
正の相関
正の相関は、相関関係があり、「一方が変化すると、もう一方も同様に変化する」ことを指します。この時、相関係数は関係が強いほど1に近い数値となり、正の値となります。
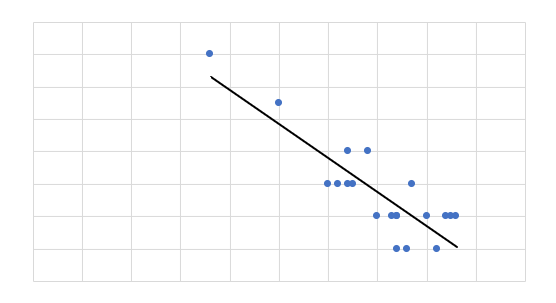
負の相関
負の相関は、相関関係があり、「一方が変化すると、もう一方は反対に変化する」ことを指します。この場合は、相関係数は関係が強いほど-1に近い値となり、負の値となります。
無相関
無相関とは、「片方の数値が変化したとしても、もう一方の値に影響が見えない」ことを指します。この場合は相関係数は0になります。
相関分析と回帰分析の違い
ここでは、相関分析と回帰分析の違いについて説明します。
ここで比較する回帰分析ですが、回帰分析とは「相関関係や因果関係があると予測されている変数に対して、その要因となる説明変数を用いて、結果を表す目的変数の影響有無を予測、分析を行う」手法をいいます。また、説明変数が1つの場合は「単回帰分析」、2つ以上の場合は「重回帰分析」といいます。
相関分析についても、影響を与えると予測した変数と目的変数の関係性を確認する分析手法という意味では共通していますが、あくまでも相関分析は影響を与える説明変数の変数予測を行うことが目的とされます。
そのため、相関分析は相関関係はあっても因果関係については問題ではなく、回帰分析は因果関係があるという点が大きく異なります。
相関分析の有効な使い時
では、相関分析はどういった分析予測を行う際に有効とされるのでしょうか。
2つの変数の関係性があることを客観的に確認したいとき
まずは「2つの変数の関係性があることを客観的に確認したいとき」です。
根本的な要因は見えていないが、関係がありそうな変数同士を相関分析で行うことによって、人の主観判断ではなく、数値として確認することが可能です。
膨大なデータ項目から関係のある変数を抽出したいとき
続いて、「膨大なデータ項目から関係のある変数を抽出したいとき」です。膨大なデータ項目同士で相関分析を行うことで、関係性のある項目を抜き出すことが可能となります。例えば、大量のtoC商材を販売する企業において、各商材同士を相関分析することで、「a商材の販売戦略を検討する際はd商材、e商材を確認すれば良い」といったような関係性を読み解くことができるかもしれません。
相関分析のやり方と流れ
相関分析の有効性が確認できたので、続いては相関分析の方法と流れについて確認します。実際に分析を行う際の流れは、「散布図の作成」「近似曲線の作成」「相関係数の算出」「相関係数の検証」です。
散布図の作成
散布図は、縦軸と横軸にそれぞれ変数を設定し、それぞれの数値を平面上に記載した図のことです。散布図は、データのばらつきを確認可能であり、相関関係がありそうか否かについても確認することができます。そのため、設定した変数の関係性について分析の余地があるか否かについて確認するために、まず散布図を作成することは非常に重要です。
近似曲線の追記
近似曲線とは、各データが数学的に関係があるか否かを確認するために散布図の上に妥当と思われるラインを描画したものを指します。近似曲線とは1に近づくほど実際のデータとのズレはなくなり、近似曲線=1の場合は、完全に近似曲線の上に実データがのる形になります。
相関係数の算出
近似曲線の作成まで終われば、いよいよ相関係数の算出です。相関係数の算出方法は、下記手順に沿って求めることが可能です。
①それぞれの変数の平均値を求める
②それぞれの変数の偏差(数値-平均値)を求める
③それぞれの分散(偏差の二乗平均)を求める
④それぞれの変数の標準偏差(分散の正の平方根)を求める
⑤共分散(偏差の積の平均)を求める
⑥共分散を2つの変数の標準偏差で割って相関係数を得る
検証
最後に、算出した相関係数の検証を行います。相関係数は1に近づく程正の相関が強く、-1に近い場合は負の相関がつよくなるため、この基準に沿って分析結果を確認しましょう。
エクセルを用いた相関分析のやり方
1. データの準備
まず、相関分析を行いたいデータをエクセルに入力します。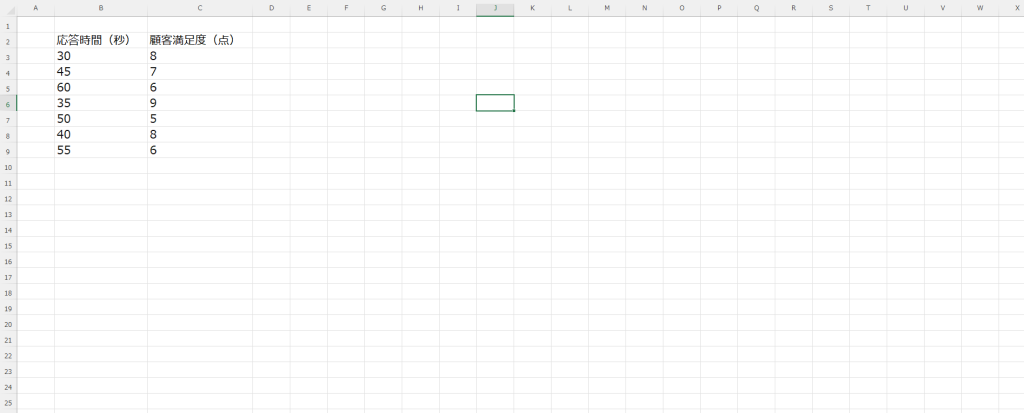
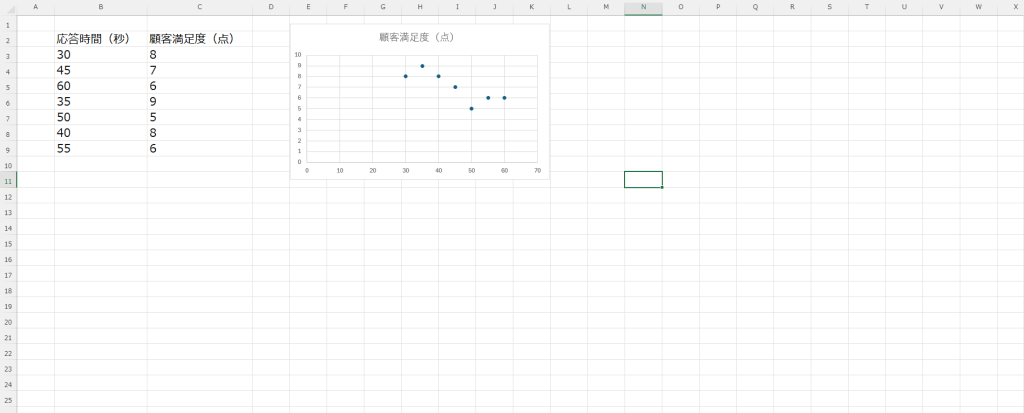
2. 散布図の作成
相関関係を視覚的に確認するために、散布図を作成します。
- データを選択: 応答時間と顧客満足度のデータ範囲を選択します。
- 挿入タブをクリック: 「挿入」タブをクリックし、「散布図」を選択します。
- 散布図を挿入: 散布図を挿入し、データの分布を確認します。
方法1: 分析ツールを使用する
- 分析ツールを有効化: 「ファイル」→「オプション」→「アドイン」→「Excelアドイン」→「分析ツール」にチェックを入れて「OK」をクリックします。
- データタブをクリック: 「データ」タブをクリックし、「データ分析」を選択します。
- 相関を選択: 「相関」を選択し、「OK」をクリックします。
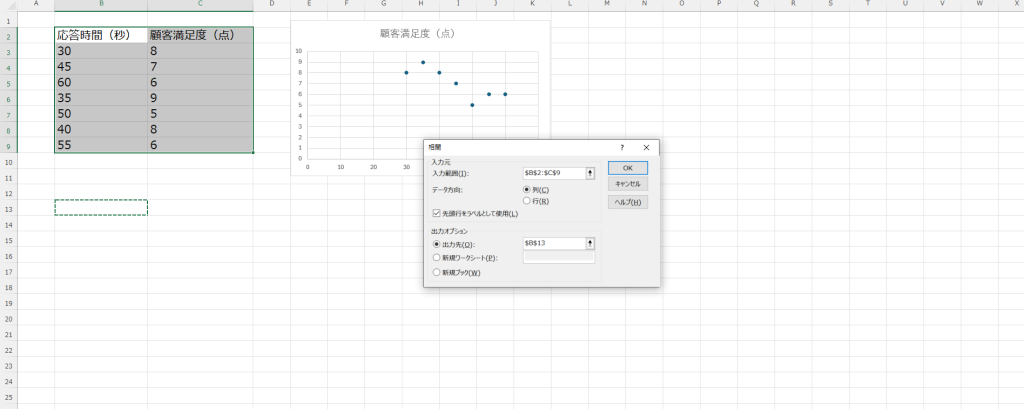
- 入力範囲を指定: 応答時間と顧客満足度のデータ範囲を指定し、「OK」をクリックします。
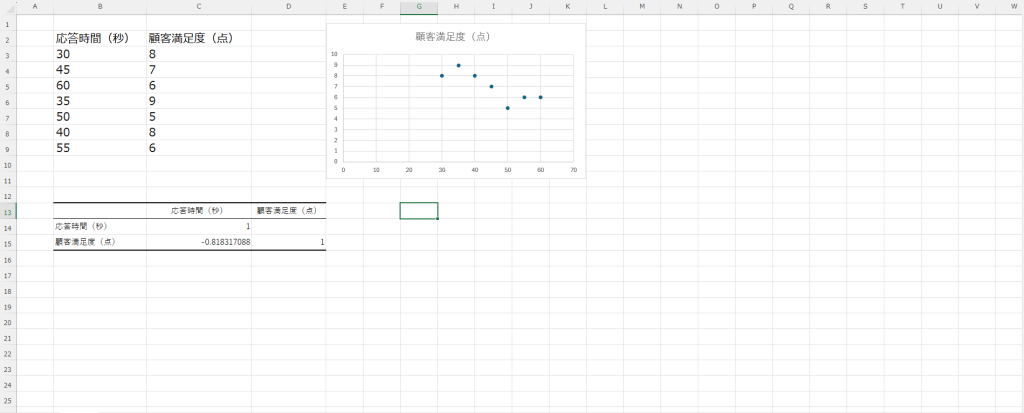
方法2: 関数を使用する
- CORREL関数を使用:
=CORREL(B2:B8, C2:C8)を入力します。
相関係数が計算されます。例えば、相関係数が -0.8だった場合、これは応答時間が長くなるほど顧客満足度が低くなる強い負の相関を示しています。
相関分析を行う際の注意点
ここでは相関分析を行う際の注意点について触れます。注意点としては「分析目的の理解」「外れ値の存在」「あくまでも直線での関係性に過ぎない」という3点があります。
因果関係を計るものではない
まず分析目的の理解については、相関分析は「因果関係を計るものではない」という点です。ここまで述べてきた通り、相関分析はあくまでも数値間の正の関係、負の関係、関係なしといった、確認を行うことを目的とした分析手法であり、根本的な要因分析ではないことを理解しましょう。
外れ値の存在
また、「外れ値の存在」にも注意することが必要です。相関分析は、以上に大きかったり小さかったりする値を表す外れ値に左右されやすく、1つでも外れ値があると相関係数が大きく変化したりすることがあります。そのため、しきい値を設定して外れ値を削除するなどの工夫が必要です。
ただ、外れ値については、個別にデータ確認を行い、外れ値の要因分析を行うことは、一般的な考察とは異なるが、新たな視点や知見となる場合もあるため、分析を行う上で注意点とはなりますが、重要な指標でもあります。
直線的な関係しか確認することができない点
最後に、相関分析では「直線的な関係しか確認することができない点」が挙げられます。具体的には比例・反比例関係については相関分析で確認可能ですが、非直線的な関係制については説明することができません。相関分析は直線的な関係を説明する分析手法と理解しておくと良いでしょう。
相関分析の事例
相関分析の具体的な事例として、気温とアイスクリームの売上の関係を考えてみましょう。
【背景】
夏になるとアイスクリームの売上が増えるという現象はよく知られています。この現象をデータで確認するために、相関分析を用います。
【データ収集】
まず、ある都市の1年間の毎日の平均気温とアイスクリームの売上データを収集します。例えば、1月1日の平均気温が5℃でアイスクリームの売上が100個、1月2日の平均気温が6℃で売上が120個、といった具合です。
【散布図の作成】
次に、収集したデータを用いて散布図を作成します。横軸に平均気温、縦軸にアイスクリームの売上をプロットします。この散布図により、気温が上がるにつれてアイスクリームの売上が増加する傾向が視覚的に確認できます。
【相関係数の算出】
散布図を作成した後、相関係数を算出します。相関係数は-1から1の間の値を取り、1に近いほど強い正の相関を示します。この場合、気温とアイスクリームの売上の相関係数が0.8であれば、強い正の相関があると言えます。
【結果の解釈】
相関係数が0.8であることから、気温が上がるとアイスクリームの売上も増加するという強い関係があることがわかります。ただし、相関関係が因果関係を示すわけではないため、他の要因(例えば、休日や特別なイベント)が売上に影響を与えている可能性も考慮する必要があります。
業務効率化ならコラボスにご相談ください
弊社では、様々な変数と事象の関係性について分析を行い、顧客の購買行動にどういった属性が影響を及ぼしているのかを確認する分析ツールについてもご提供させて頂いております。こういった分析・解析ツールにご興味がございましたら、是非お問い合わせ、ご相談頂けますと幸いです。
まとめ
本記事では相関関係や相関分析について、言語理解や分析手法も含めてご説明しました。企業の売上拡大において、どういった変数が何に影響があるのかといった変数について確認や分析を行うことで販売促進の効率化に繋がるのではないでしょうか。
本記事でご説明いたしました内容についてのお問い合わせやご相談事項につきましては、ご遠慮なくお問い合わせやお電話にてご連絡頂けますと幸いです。
この記事の執筆者
コラボスブログ編集部
株式会社コラボスは、2001年に設立。現在、東京・大阪にオフィスを構えており、
960拠点以上のお客様へクラウドサービスを使ったCTIシステムを提供。
本ブログ記事サイトでは、様々なニーズを抱えたお客様のお役に立てるような情報を日々発信。
会社情報について詳しくはこちら







